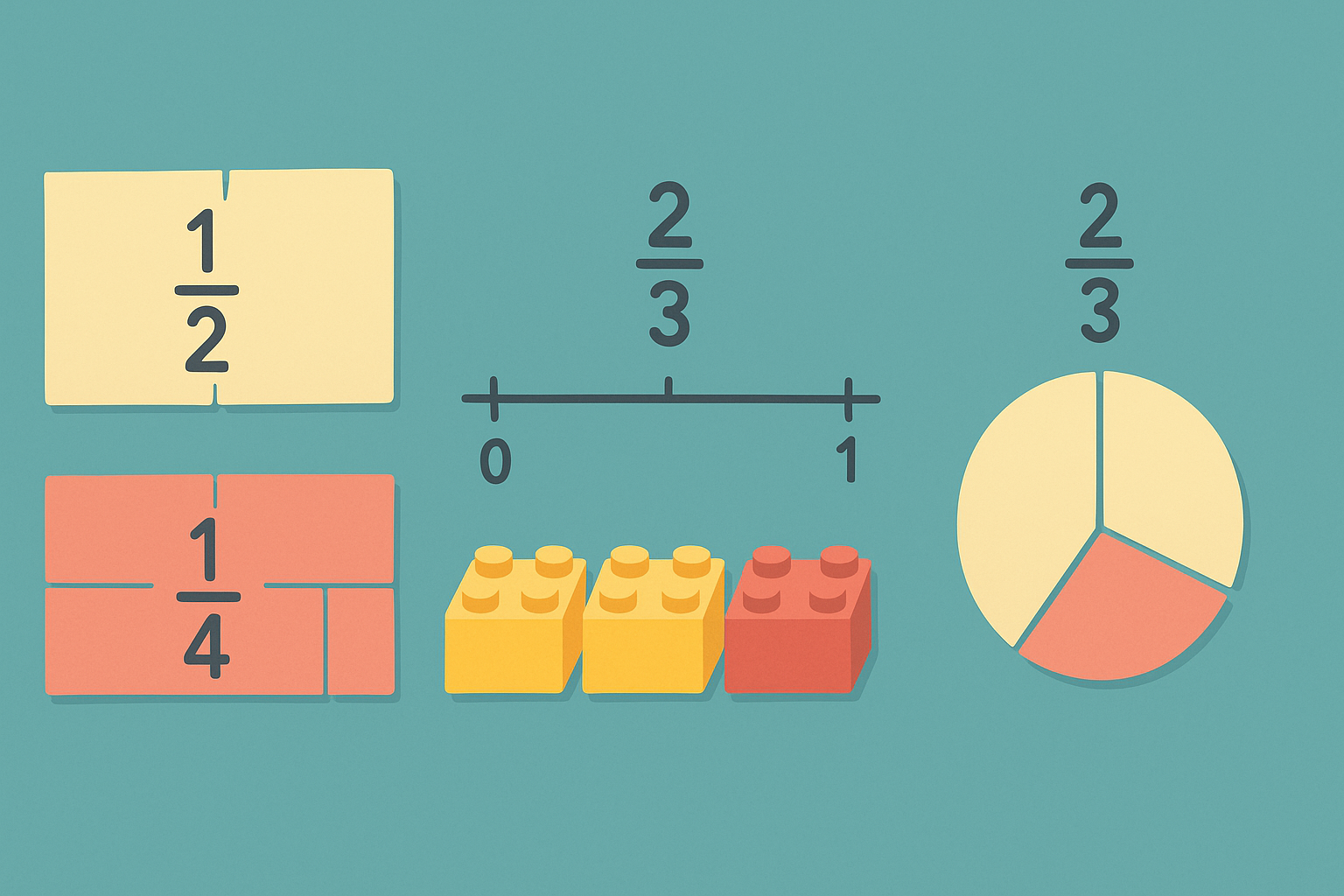はじめに
分数の計算は、小中学校の数学の中でも「難しい」と感じる人が多い分野です。なぜ、分数はこんなにもとっつきにくく感じられるのでしょうか。その背後には、分数の持つ抽象性、日本語と数式の表現の違い、さらに実生活との接点の少なさといった、いくつもの要因が関係しています。
本記事では「分数の計算が難しい理由とその学び方」をテーマに、まず分数に対して苦手意識を持ちやすい原因を掘り下げ、その後に効果的な勉強方法や克服のためのポイントを紹介します。この記事が、分数への苦手意識を和らげ、学習の理解や意欲を高める一助となれば幸いです。
第1章:なぜ分数の計算が難しいのか
1-1. 分数の抽象的な性質
分数とは「ある全体を等しく分けた一部の量」を表す数です。たとえば、ケーキを4等分してそのうちの1つを取れば「4分の1」となります。一見シンプルですが、整数と違って「何等分か」「何個分か」といった情報を同時に把握する必要があるため、頭の中での処理が複雑になります。
さらに、「1/2=0.5」や「1/4=0.25」のように、小数との対応も理解しなければならず、分数は一つの数を複数の見方で捉える力が必要です。また、「約分」や「通分」といった特有の操作が頻繁に出てくるのも難しさの一因です。これらの手順を整理して体系的に学ばないと、分数の計算がますます難しく感じられるようになります。
1-2. 日本語と数学表現のギャップ
分数は日常でも「半分」「4分の1」などの形で耳にしますが、数学では「a/b」といった形式で扱われます。このように、日本語では回りくどく、数学では簡潔な表現になるため、言語と視覚のズレが理解の障壁となることがあります。
加えて、「%(パーセント)」や「割・分(歩合)」など、日本語特有の数の表現も混在するため、分数・小数・百分率を相互に変換する必要があります。これらを使い分ける負担が、学習者にとっては大きなハードルとなります。
1-3. 実生活とのつながりの薄さ
分数は本来、ケーキやピザの分け方など、生活に根ざした概念です。しかし、日常生活で分数を使う機会は少なく、意識的に取り入れなければ実感を伴った理解にはつながりにくいのが現実です。
例えば料理の分量で「1/2カップ」などの表記はありますが、料理を日常的に行わない子どもにとっては、学習への応用が難しくなります。また、家計簿や割引などの実用計算では分数よりも小数やパーセンテージが使われがちで、分数に触れる機会自体が減っているのです。
1-4. 苦手意識の早期定着
算数に苦手意識を持っている子どもは、分数のような手順の多い計算で早い段階からつまずくことがあります。「自分は分数ができない」という思い込みがモチベーション低下を引き起こし、さらに理解不足に拍車をかけるという悪循環に陥りがちです。
特に、手順が複雑な分数計算は「わからない→できない→嫌い」という負のサイクルが起こりやすく、放置していると高校数学以降の「分数方程式」や「分数関数」にまで影響が及びます。早めの理解と苦手克服がカギとなります。
第2章:分数計算の基本とつまずきやすいポイント

2-1. 約分と通分の基本
分数計算の基礎は「約分」と「通分」です。
-
約分:分子と分母に共通の因数がある場合、それを取り除いてシンプルにする操作(例:6/8 → 3/4)
-
通分:分母を揃えて、加減算を可能にする操作(例:1/2+1/3 → 3/6+2/6)
つまずきやすいのは、「いつ約分するのか」「どこで通分すればいいのか」が分からないケースです。練習を通して、それぞれの手順を自然に使えるようにしておくことが大切です。
2-2. 足し算・引き算の注意点
分数の加減算では、必ず分母をそろえる必要があります。これが、整数の感覚になれていると非常に面倒に感じられます。
例:
23+15=1015+315=1315\frac{2}{3} + \frac{1}{5} = \frac{10}{15} + \frac{3}{15} = \frac{13}{15}32+51=1510+153=1513
このように最小公倍数を求め、分子を同じ比率で拡張するという一連の手順を理解し、慣れておく必要があります。間違って「2+1=3」と単純に加えると、答えがまったく異なってしまいます。
2-3. 掛け算と割り算のコツ
分数の掛け算は、分子と分母をそれぞれ掛けるだけの簡単な操作です。
ab×cd=a×cb×d\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}ba×dc=b×da×c
一方、割り算は「逆数を掛ける」に変換する必要があります。
ab÷cd=ab×dc\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}ba÷dc=ba×cd
この変換に納得していないまま暗記で済ませてしまうと、「なぜ掛け算に変えるのか」が理解できず、応用が効かなくなります。逆数の考え方をきちんと学ぶことが重要です。
2-4. 複雑な式に対する対応力
分数を含む複雑な式になると、通分・約分・加減乗除がすべて絡み合うため、混乱しやすくなります。
例:
23+1−12×34\frac{2}{3} + 1 – \frac{1}{2} \times \frac{3}{4}32+1−21×43
例:
34÷(1+12)\frac{3}{4} \div (1 + \frac{1}{2})43÷(1+21)
これらの式も、一つ一つの操作は基本的な分数計算の延長です。重要なのは「順を追って丁寧に分解する」力です。計算の順番、約分のタイミング、通分の要否などを正しく判断することで、複雑な問題にも対応できるようになります。
第3章:分数計算を克服するための学習法
3-1. 具体物を活用した体験型学習
分数の理解を深めるには、実際に「目で見て」「手で触れる」体験が非常に効果的です。特に学習初期の段階では、紙を切って「1/2」や「1/4」を作ったり、ブロックやおはじきを並べて「3/5」を表現したりすることで、抽象的な分数を視覚的・感覚的に捉えやすくなります。
このような体験型の学習は、単なる計算練習に比べて記憶に残りやすく、理解の土台を築くのに最適です。また、すでに苦手意識がある場合でも、原点に立ち返って具体物を使った学びを取り入れることで、これまで見落としていたポイントに気づくことがあります。
3-2. 数直線や図解を活用した視覚的理解
分数の概念を明確にするうえで、数直線やモデル図の活用も非常に有効です。たとえば「1/2」は0と1のちょうど中間、「2/3」は0から1の間を3等分してそのうち2つ分というように、数直線に配置することで、数の大きさや位置関係を直感的に把握できます。
また、長方形を使った図解(モデル図)では、分数の加減を視覚的に表現できます。たとえば「色を塗って足す」「塗りつぶされた部分を引く」といった操作を視覚的に捉えることで、計算手順が頭の中で整理されやすくなります。図を使った学習は、抽象的な数字に苦手意識を持っている生徒の理解を助ける強力なサポートになります。
3-3. 小数・パーセントとの変換で理解を深める
分数に苦手意識がある一方で、小数やパーセントなら理解しやすいという人も少なくありません。そこで、分数・小数・パーセントの相互変換を意識して練習することで、各表現の関係性が見えてきます。
例えば、「1/2」は「0.5」や「50%」と同じ意味だと繰り返し確認することで、感覚的な理解が進みます。こうした変換練習を通じて、単なる計算だけでなく、「なぜこの表現を使うのか」「それぞれの利点は何か」といった数学的な背景にも触れられるようになり、学習への関心も高まります。
3-4. 計算の手順を明確化し、繰り返し練習する
分数計算には、「通分」「約分」「計算」「答えの整理」といった明確なステップがあります。これらを正しく理解し、繰り返し実践することで、自然と計算の流れが身につきます。
おすすめの方法は、「自分の計算過程を言葉で説明する」練習です。たとえば、「まず分母をそろえる」「次に分子を計算する」「最後に約分する」と声に出しながら手を動かすことで、理解が深まり、記憶にも定着しやすくなります。反復練習と論理的な説明を組み合わせることで、計算への自信が養われます。
3-5. 計算ドリルで徹底的に反復練習
分数計算を定着させるには、数をこなす反復練習が欠かせません。中学以降の数学では分数の応用力が問われる場面も増えるため、段階的なドリル学習が効果的です。
-
基礎レベル:分母が同じ分数の足し算・引き算、簡単な掛け算・割り算
-
標準レベル:異なる分母の加減算、分数同士の掛け算・割り算
-
応用レベル:文字式を含む分数、複数の演算が混在する式、文章題
練習では途中式を丁寧に書き、ミスを振り返る習慣をつけましょう。間違えた理由を明確にすることで、次回のミスを防ぐことができます。
3-6. 日常生活の中で分数を意識してみる
分数に対する苦手意識は、「実生活との関わりの薄さ」が原因であることも多いです。だからこそ、日常の中で分数を意識的に取り入れることで、実感を伴った理解が得られます。
-
料理:「1/2カップ」「1/4小さじ」などの分量を実際に測って使う
-
買い物:割引表示の「1/2価格」や「1/3オフ」を見たときに小数や%に換算してみる
-
おこづかい管理:「今月は1/3を貯金に」「1/6を趣味に」と割合で使い分ける
このように身近な場面で分数を見つけて活用することで、数学が「机上の勉強」から「使える知識」へと変わり、学習意欲も自然と高まります。
第4章:分数学習に役立つ補助教材とデジタルツール
4-1. アプリやオンライン教材の活用
最近では、分数計算に特化した学習アプリやオンライン教材が豊富に提供されています。ゲーム感覚で楽しみながら計算練習ができるアプリ、動画付きで丁寧に解説してくれる教材など、目的に応じた選択肢が広がっています。
特におすすめなのは、「間違えた問題を自動で分析し、弱点を補強してくれる機能」があるツールです。効率的に苦手を克服できます。ただし、単に問題数をこなすだけでは誤ったクセが定着する可能性もあるため、「なぜ間違えたのか」をきちんと確認できる教材を選ぶようにしましょう。
4-2. 解説動画やオンライン個別指導の活用
「文章だけでは理解しづらい」という場合は、解説動画の視聴がおすすめです。講師の説明を聞きながら、計算の流れをリアルタイムで追うことができ、特に視覚・聴覚を同時に使うことで理解が深まります。
さらに、自分に合った個別指導を受けたい場合は、オンライン個別指導サービスを利用するのも一つの方法です。講師とリアルタイムでやり取りできるため、疑問点をすぐに解消でき、計算のどこでつまずいているかを一緒に確認しながら進めることができます。
4-3. グループ学習や勉強会の効果
一人での学習に限界を感じたら、グループでの学びにもチャレンジしてみましょう。分数計算のように手順が多い学習では、他の人と一緒に取り組むことで、新たな発見や理解の深化が得られます。
-
他人の解き方から学べる:同じ問題でも、人によって計算手順が異なるため、新しい視点を得られる
-
教え合いで理解が深まる:他の人に説明することで、自分の理解の曖昧さに気づける
勉強会では、答えを出すことに加えて「なぜその方法を使ったか」などを説明し合うと、より実践的な力が身につきます。
第5章:分数計算に向き合うための心理的アプローチ

5-1. 苦手意識を乗り越えるための心の持ち方
「分数は難しい」「自分にはできない」といったネガティブな思い込みは、学習意欲を下げ、理解の妨げになります。こうした先入観を持たないよう、まずは「分数計算は手順さえ分かれば解けるもの」「最初に苦戦するのは誰でも同じ」と前向きにとらえる姿勢を持つことが大切です。
また、初めから完璧を目指すのではなく、簡単な問題からスタートして「できた!」という成功体験を積み重ねていくことが、モチベーション維持の鍵となります。成功の感覚を少しずつ増やしていくことで、自然と自信が育まれ、難しい問題にも挑戦しやすくなります。
5-2. 小さな目標を立てて達成を積み重ねる
一度に大きな成果を目指すのではなく、「今日は通分の練習をする」「明日は掛け算だけに集中する」など、学習内容を小さなステップに分けて取り組むことで、継続しやすくなります。短時間でも集中して取り組める目標を設定することで、達成感を味わいやすくなり、やる気の持続にもつながります。
さらに、目標を達成したら、達成感を自分自身でしっかり味わいましょう。シールを貼る、チェックリストを埋める、ご褒美を用意するなど、視覚的・感覚的に「やりきった」ことを実感できる工夫が効果的です。この積み重ねが、分数に対する心理的なハードルを徐々に下げていきます。
5-3. 失敗から学びを得る力を育てる
ミスをしたときこそ、学びのチャンスです。「できなかった自分」を否定するのではなく、「なぜ間違えたのか?」を振り返ることが、次の成長につながります。たとえば以下のような視点から分析してみましょう:
-
約分のタイミングを見落としたか?
-
通分後の分子の計算でミスしたか?
-
計算の順序(演算のルール)を誤解していたか?
-
割り算で逆数をかける操作を忘れていたか?
こうした反省を記録に残すことで、同じタイプの問題に再び出会ったときに注意するポイントが明確になります。失敗を前向きに捉え、次に活かす姿勢が、着実な理解と実力アップへとつながります。
第6章:分数計算が活きる他分野とのつながり
6-1. 方程式や関数への発展的応用
中学・高校へと進むと、分数は方程式や関数の中でも頻繁に使われます。たとえば、
x2+1=3×4\frac{x}{2} + 1 = \frac{3x}{4}2x+1=43x
といった式では、分母をそろえて計算を進める必要があります。また、1/x のような「分数関数」も高校で登場し、グラフの形や定義域などを考えるうえで分数の性質を理解しておくことが欠かせません。
分数計算を「丸暗記の手順」として扱ってしまうと、これらの応用問題で対応できなくなります。逆に、論理的に理解しておけば、より複雑な問題にもスムーズに対応でき、数学全体への理解も深まります。
6-2. 割合・比の問題や文章題との関係
分数が表立って登場しなくても、割合や比を使った文章題の中には、分数の概念がしっかりと組み込まれています。たとえば「全体の3/5を使用した」「1/4が減少した」といった表現は、分数の理解がなければ正しく式に落とし込めません。
また、「30%引きの商品はいくらになる?」といった問題も、小数では「0.7をかける」と計算できますが、本質的には「1 – 30/100」という分数表現と同じ意味です。割合や比率に強くなるためには、分数の感覚をきちんと養うことが前提条件となります。
6-3. 理科(物理・化学)における計算力の土台
分数の扱いに慣れていると、理科系科目での計算がスムーズに進みます。物理では速度や加速度の計算、化学では濃度や反応比などの計算で、単位換算や分数の取り扱いが頻繁に求められます。
たとえば、溶液の質量と体積の割合を求める濃度計算や、速度の式で時間や距離を分数として処理する場面では、分数に対する理解が計算の正確性とスピードを左右します。逆に分数計算が不安定だと、理科の計算問題で不必要なミスを招きやすくなります。
第7章:まとめとこれからの学びに向けて
分数の計算が難しいと感じられるのは、決して個人の能力の問題ではありません。分数という概念がもともと抽象的であり、日本語の表現との違いや、日常生活との接点の少なさ、計算手順の複雑さなど、さまざまな要因が複雑に絡み合っているからです。
しかし、こうしたハードルは決して乗り越えられないものではありません。紙やブロックなどの具体物を使った体験的な学習、数直線や図解による視覚的理解、小数やパーセントとの変換を取り入れた応用学習など、工夫次第で分数はぐっと身近な存在になります。
また、近年では学習アプリやオンライン教材といった便利なツールも充実しており、自分の苦手な部分を集中的に克服したり、繰り返し練習したりすることが可能です。グループ学習や勉強会など、他の人と学ぶ機会を活かせば、新たな気づきや刺激を得られることもあるでしょう。
心理面でも、「分数が苦手」と思い込まず、まずは小さな成功を積み重ねていくことが大切です。失敗しても落ち込むのではなく、「どこでつまずいたか」を丁寧に振り返る習慣をつけることで、着実に理解が深まっていきます。
分数の計算力は、中学・高校の数学にとどまらず、理科、統計、経済といったさまざまな分野に応用が利く基礎的なスキルです。しっかりと身につけておくことで、その先の学びがずっとスムーズになります。一方で、分数に苦手意識を持ったままだと、今後の学習全体に大きな影響を与えかねません。
だからこそ、「今、少し自信がないな」と感じている人こそ、焦らず一歩ずつ基礎に立ち返ってみることをおすすめします。アプリでの自習、動画による解説、先生や家庭教師のサポートなど、自分に合った方法を取り入れながら、無理のないペースで学び直してみましょう。
分数は、決して特別な人だけが理解できるものではありません。正しい手順を踏み、丁寧に練習を重ねていけば、誰にでもきちんと習得できるものです。
本記事では、「分数の計算が難しく感じられる理由」と、それを乗り越えるための多様な学習アプローチをご紹介してきました。分数は、整数とは異なる独自の考え方を必要とするテーマですが、その分、理解を深めることで計算の幅が広がり、より高度な数学にも自信をもって取り組めるようになります。
この内容が、少しでも分数へのハードルを下げ、「やってみよう」と思えるきっかけになれば幸いです。分数を乗り越えた先には、新しい学びの世界が広がっています。たとえ困難に感じる場面があっても、挑戦する過程そのものが、あなたの学びを深く、豊かにしてくれるはずです。